• Motivation
• Parsl Primitives
• Composing a workflow in Parsl
• Gory details
• Conclusion
• Foonotes/Bibliography

Motivation

Imagine you have a computation expressed in Python that has asynchronous tasks that are inherently parallelizable. What do you do? Maybe you reach for threading, but that’s a mistake since in Python threads can’t run in parallel (thanks GIL 😠). Maybe you reach for multiprocessing. That’d be a valid solution as long as you’re comfortable writing such code, which often involves synchronization logic, and you don’t need to distribute across compute resources. But, what if you don’t want to worry about low-level code and in fact you want to distribute to 10, 100, or 1000 possibly heterogenous compute nodes? For that use case, you should probably reach for Parsl.

Some examples of the kind of work that Parsl ends up being a useful tool for:

• DNA sequence analysis, which is computationally-intensive, data-intensive, and requires fault tolerant and efficient utilization of infrastructure across multiple compute nodes and even sites
• X-ray microtomography to characterize the neuroanatomical structure of brain volumes, for example at the Argonne Advanced Photon Source where work is outsourced to Argonne’s Leadership Computing Facility
• Cosmology simulation, for example to simulate images from each of the Large Synoptic Survey Telescope’s 189 sensors

Parsl Primitives

Parsl (parallel scripting library) is a Python package that makes defining and executing parallel computations ergonomic. Parsl’s principal value proposition is management and scheduling of asynchronous and concurrent tasks in fault tolerant ways, at exascale. It delivers on this proposition by exposing exceedingly simple primitives that can be composed functionally to build workflows. The paramount primitives¹ are a decorator python_app, which wraps conventional² Python functions

@python_app
def hello():
    return 'Hello World!'

and an abstraction for operating on file-like objects called File

@python_app
def sort_numbers(inputs=[]):
    with open(inputs[0].filepath, 'r') as f:
        strs = [n.strip() for n in f.readlines()]
        strs.sort()
        return strs

unsorted_file = File('unsorted_numbers.txt')

f = sort_numbers(inputs=[unsorted_file])

Each Python function wrapped by python_app (generally called an app) returns either an AppFuture or a DataFuture (depending on whether an app produces a File as the product of the task), each of which inherit and extend concurrent.futures.Future. Therefore execution of an app is asynchronous and results need to await³ resolution:

@python_app
def hello():
    import time
    time.sleep(5)
    return 'Hello World!'
...
>>> app_future = hello()
# Check if the app_future is resolved, which it won't be
>>> print('Done: {}'.format(app_future.done()))
Done: False
# Print the result of the app_future. Note: this
# call will block and wait for the future to resolve
>>> print('Result: {}'.format(app_future.result()))
Result: Hello World!
>>> print('Done: {}'.format(app_future.done()))
Done: True

Composing a workflow in Parsl

With these primitives in hand, which you can compose, you’re ready to build arbitrarily complicated workflows. For example suppose you wanted to estimate a quantity; in particular the integral $I$ of a nontrivial integrand

Under fairly weak assumptions⁴ (that our integrand satisfies) we know by the Strong Law of Large Numbers that

where $f(x) = \frac{\sin x}{x + \cos^2 x}$ and $U$ is a random variable distributed uniformly. This naturally suggests itself to being implemented as an “embarassingly parallel” computation: draw lots of samples from the uniform disitrubtion, apply $f$ to each sample, then average the result. We can implement this workflow in a straightforward way using Parsl primitives:

@python_app
def monte_carlo():
    from random import random
    from math import sin, cos
    u = random()
    return sin(u) / (u + cos(u)**2)

@python_app
def mean(inputs):
    return sum(inputs)/len(inputs)
...
>>> n_draws = 100
>>> fus = [monte_carlo() for _ in range(n_draws)]
>>> integ = mean(inputs=fus)
>>> print("Average: {:.5f}".format(integ.result()))
Average: 0.35094

This result is considerably different from the correct answer as computed by a numerical integrator (0.36358 to five decimal places) owing to the paltry number of draws. We can certainly remedy this by increasing the number of draws but on a single machine (or a single core) we would just be linearly increasing the runtime. Parsl raison d’être is scaling this workflow (and those much more complicated) up to ~100,000 parallel workers, such that absolutely no amendment to the logic of the computation is necessary on your part.

Gory details

How does Parsl work? The best discussion of the internals can be found in Babuji et al. but briefly Parsl is built on top an execution management engine called DataFlowKernel that manages tasks scheduling and tasks dependencies (represented as a graph). In order to make itself more accessible to a typical scientific user, Parsl also wraps several interfaces available on scientific clusters and supercomputers as Providers; currently, Parsl implements Providers for Slurm, Torque/PBS, HTCondor, Cobalt, GridEngine, AWS, Google Cloud, Jetstream, and Kubernetes. Parsl also wraps the job launchers fork, srun, aprun, mpiexec, GNU parallel as a Launcher.

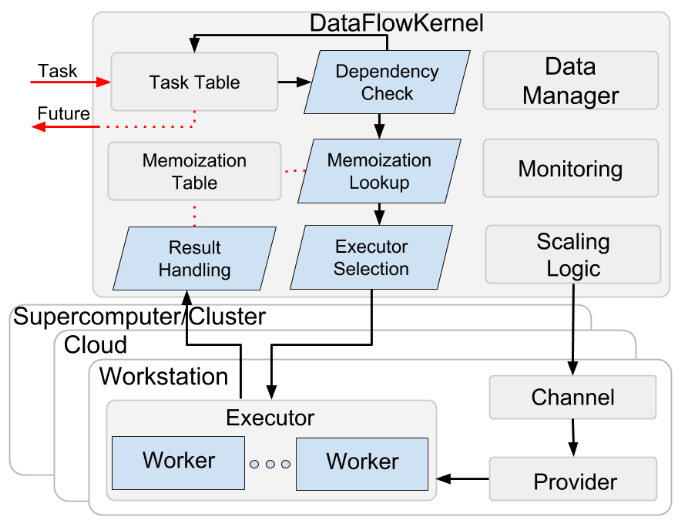
To support diverse execution requirements (e.g. high throughput vs. low latency) Parsl provides a modular Executor interface and implementations that support three common use cases:

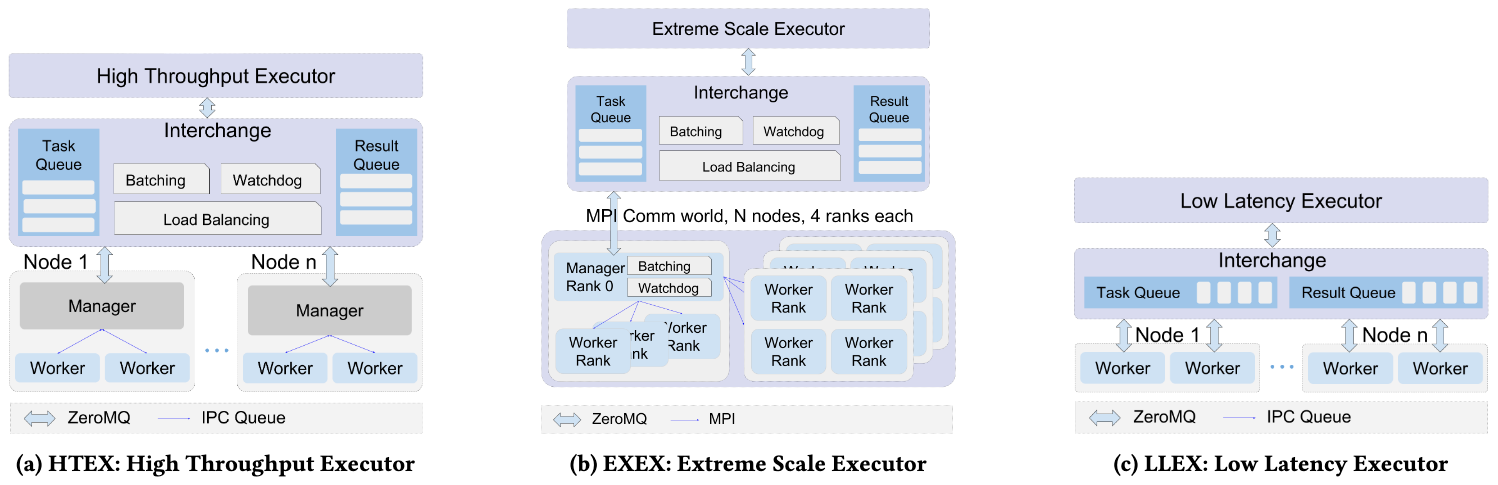
More about the implementation can be found in the Parsl paper, along with evaluation and comparison against similar tools.

Conclusion

Parsl is great if you want to do a lot of work in parallel but don’t want to write all of the bookkeeping and scheduling code yourself! As already mentioned a deeper technical discussion is available in the Parsl paper. Documentation is available at the Parsl project homepage and you can even experiment with it right now in your browser using the project’s provided binder instance. The project is open source and very welcoming of PR submissions.

Foonotes/Bibliography